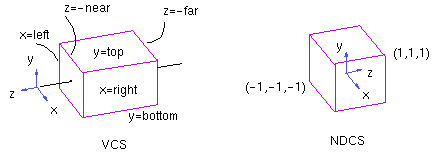
The general purpose of the projection transformation is to map a 3D
point in VCS to a 2D point in NDCS. However, having a z-coordinate in NDCS
allows us to do visibility calculations, so the point in NDCS will be 3D
as well.
Orthographic Projections
Orthographics projections require only scaling and translation and are
therefore the simplest.
We begin by looking at the desired transformation for the y coordinate.
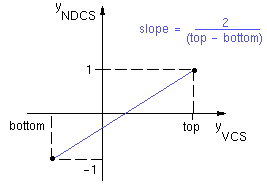
y' = 2y/(top-bottom) - (top+bottom)/(top-bottom).
Similarly,
x' = 2x/(right-left) - (right+left)/(right-left).
Lastly, we do the same for z. We wish top map z=-near to z'=-1 and z=-far
to z'=1. Note that the new z' axis points in the opposite direction --
NDCS is a left-handed coordinate system.
z' = -2z/(far-near) - (far+near)/(far-near).
Placing this all in a matrix gives:
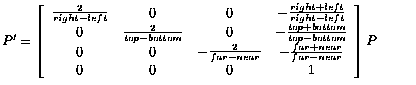
OpenGL Calls for Orthographic Projections
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
followed by one of:
glOrtho(left, right, bottom, top, near, far)
gluOrtho2D(left,right,bottom,top)
In the above, near>0 and far>0 set the clipping planes at z=-near and z=-far.
The function call gluOrtho2D() is the same as calling glOrtho()
with near=0 and far=1.
Perspective Projections
Perspective projections are more commonly used and require some additional
effort to derive.
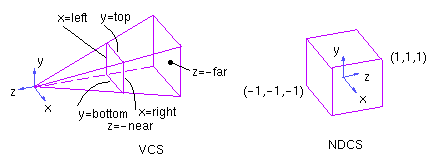
The first step is choosing the form of the matrix. A simple version
which projects onto the plane given by z=-d was given earlier by
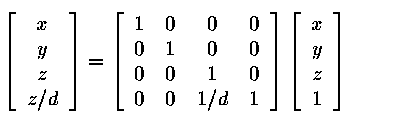The more complex transformation we wish to perform will in addition need
the ability to scale and translate each of x, y, and z. The following matrix
has all the correct elements in place.
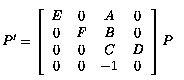
The choice of the coefficient of -1, which makes h' = -z, is arbitrary.
Scaling this number can be matched by scaling each of the other parameters.
Let's first look at how y gets mapped to y'. For y = -z*top/near, we
would like y'/h' = 1. Thus,
(-F*z*top/near + B*z)/(-z) = 1
Similarly, for y = -z*bottom/near, we would like y'/h' = -1. Thus,
(-F*z*bottom/near + B*z)/(-z) = -1
Solving these two equations for F and B gives
F = 2 near/(top-bottom)
B = (top+bottom)/(top-bottom)
The mapping for x is determined in an analogous way, giving
E = 2 near/(right-left)
A = (right+left)/(right-left)
Lastly, let's look at the mapping for z. For z=-near, we would like
z'/h' = -1. Thus
C(-near)/near + D/near = -1 .
For z=-far, we would like z'/h' = 1. Thus
C(-far)/far + D/far = 1
Solving these equations for C and D gives:
C = -(far+near)/(far-near)
D = -2*far*near/(far-near)
OpenGL calls for Perspective Projections
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
followed by one of:
glFrustum(left, right, bottom, top, near, far)
gluPerspective(fovy, aspect, near, far)
The glFrustum() call uses the parameters as described above. An
alternative specification is to use field-of-view and an aspect
ratio to specify the image plane parameters. In gluPerspective(),
fovy
gives the field-of-view in the y-direction, measured in degrees and centred
about y=0. The aspect ratio gives the relative horizontal size of the image,
centred about x=0.
Non-linearity in Perspective Transformations
The perspective transformations produce a z-coordinate for use in visibility
calculations. It is, however, a non-linear function of the original z coordinate.
To illustrate this, consider a railroad viewed in perspective as follows.
tracks
left: x= -1, y= -1
right: x= 1, y= -1
view volume
left = -1, right = 1
bot = -1, top = 1
near = 1, far = 4
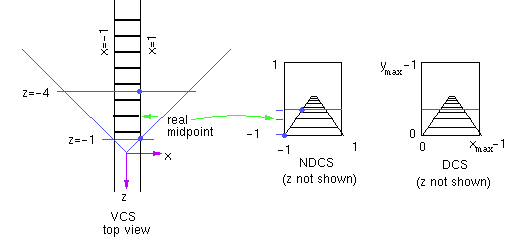In this scene, what happens to z in VCS and NDCS as we move along the track?
The following expressions tell us what we wish to know.
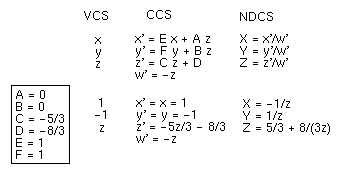
It can be directly seen that z_NDCS is a non-linear function of z_VCS.
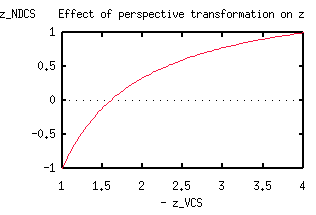
What does this look like in the image plane? Let's determine z_VCS as
a function of x_NDCS. With this we can point at the image and ask What
is the real distance of this point?
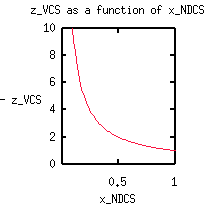
Lastly, what does the train track look like in NDCS?
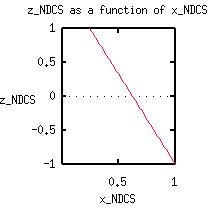
Straight lines in VCS correspond to straight lines in NDCS, although
the 'speed' at which one moves along them is not the same in the two coordinate
systems. |
