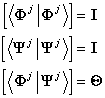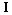 —
единичная матрица.
—
единичная матрица.
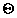 —
нулевая матрица.
—
нулевая матрица.
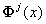 или
или 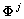 — вектор базисных функций
— вектор базисных функций 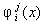 (скейлинг-функций) пространства
(скейлинг-функций) пространства 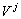 .
.
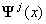 или
или 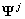 — вектор базисных функций
— вектор базисных функций 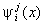 (вейвлетов) пространства
(вейвлетов) пространства 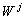 .
.
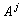 ,
, 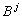 — операторы декомпозиции, выделяют соответственно низко- и
высокочастотные составляющие исходного сигнала.
— операторы декомпозиции, выделяют соответственно низко- и
высокочастотные составляющие исходного сигнала. 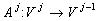 ,
, 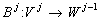 .
.
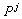 ,
, 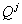 — операторы синтеза.
— операторы синтеза. 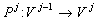 ,
, 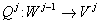 .
.
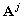 ,
, 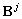 ,
, 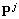 ,
, 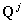 — матрицы операторов (
— матрицы операторов (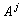 ,
, 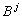 ,
, 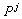 ,
, 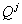 соответственно) в некоторых базисах.
соответственно) в некоторых базисах.
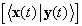 —
матрица скалярных произведений двух систем функций. Если
—
матрица скалярных произведений двух систем функций. Если 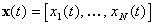 и
и 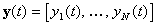 , то
матрица имеет размер
, то
матрица имеет размер 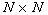 и элемент с номером
и элемент с номером 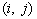 содержит значение
содержит значение 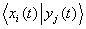 .
.
Вейвлет-анализ и его приложения
Лекция 1
Вейвлет-анализ в компьютерной графике
Введение
Рассматривается применение вейвлетов для решения четырех видов задач: обработка растровых изображений, работа с кривыми, работа с поверхностями, решение задачи глобальной освещенности методом излучательности.
Матричная запись
Матричная запись бывает в ряде случаев более наглядна, особенно если для разных участков сигнала используются различные фильтры (фильтры могут меняться, например, на границах сигнала). В этом случае не все столбцы матриц будут сдвинутыми копиями друг друга. Однако реализация "в лоб" матричной записи не всегда оказывается эффективной, так как требует предварительной генерации самих матриц, что часто оказывается весма трудоемким. Более эффективной оказывается реализация фильтров и сверток.
Используемые обозначения