- Eric J. Stollnitz, Tony DeRose, David H. Salesin. Wavelets for Computer Graphics. Theory and Applications. Morgan Kaufmann Publishers, Inc., San Francisco, California, 1996, pp. 181-194.
- Е. В. Шикин, А.В. Боресков. Компьютерная графика. Динамика, реалистические изображения. ДИАЛОГ-МИФИ, Москва, 1996, с. 258-262.
- Pat Hanrahan, David Salzman, Larry Aupperle. A Rapid Hierarchical Radiosity Algorithm. In Proceedings of SIGGRAPH’91, pp. 197-206. ACM, New York, 1991.
- Peter Schroder. Wavelet Methods for Integral Equations. In Proceedings of SIGGRAPH’94. Course Notes, #11, pp. 107-127.
- Steven J. Gortler, Peter Schroder, Michael F. Cohen, Pat Hanrahan. Wavelet Radiosity. In Proceedings of SIGGRAPH’93, pp. 221-230. ACM, New York, 1993.
- О. Ю. Кокорин, С.А. Упольников. Использование иерархического алгоритма в методе излучательности. Труды конференции ГрафиКон’97, с. 31-37, Москва, 1997.
Вейвлеты в задачах глобальной освещенности
Метод излучательности
(Функция ![]() задается геометрией сцены и определяет долю энергии, переносимую с одной
точки сцены на другую).
задается геометрией сцены и определяет долю энергии, переносимую с одной
точки сцены на другую).
Таким образом, функция B является решением интегрального уравнения. Его можно решать так. Сначала представить искомую функцию в виде разложения по некоторому базису в пространстве функций излучательности (т.е. в виде суммы ряда по соответствующим базисным функциям). Тогда задача, очевидно, сведется к решению системы из бесконечного числа линейных алгебраических уравнений. Если же рассмотреть проекцию пространства функций излучательности на некоторое конечномерное подпространство (метод конечных элементов), то проекция искомой функции в этом подпространстве будет представлена уже в виде конечной суммы. Это даст уже конечную систему уравнений. От выбора подпространства и базиса в нем будет, естественно, зависеть степень близости решения системы к реальной функции B.
Проще всего подпространства и базисы в нем выбирать так. Фиксируем
некоторое число ![]() и разбиваем всю сцену на n поверхностей (фрагментов)
и разбиваем всю сцену на n поверхностей (фрагментов) ![]() .
Получаем n-мерное подпространство пространства функций
излучательности. Базисная функция с номером i этого подпространства
равна 1 во всех точках
.
Получаем n-мерное подпространство пространства функций
излучательности. Базисная функция с номером i этого подпространства
равна 1 во всех точках ![]() и 0 во всех остальных точках. Уравнение баланса световой энергии в таком
случае сводится к системе n линейных алгебраических уравнений:
и 0 во всех остальных точках. Уравнение баланса световой энергии в таком
случае сводится к системе n линейных алгебраических уравнений:
где ![]() —
излучательность i-того фрагмента,
—
излучательность i-того фрагмента, ![]() — собственная излучательность i-того фрагмента,
— собственная излучательность i-того фрагмента, ![]() — коэффициент отражения i-того фрагмента (
— коэффициент отражения i-того фрагмента (![]() ),
), ![]() — коэффициент формы (form factor) — доля энергии j-того
фрамента, попавшая на i-тый фрагмент.
— коэффициент формы (form factor) — доля энергии j-того
фрамента, попавшая на i-тый фрагмент.
В матричной форме:
Из определения коэффициента формы и закона сохранения энергии следует,
что для любого ![]()
следовательно матрица ![]() обладает диагональным преобладанием и система решается простыми
итерационными методами, например, методом Гаусса-Зейделя.
обладает диагональным преобладанием и система решается простыми
итерационными методами, например, методом Гаусса-Зейделя.
Выпишем выражение для коэффициента формы:
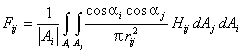 ,
,где ![]() —
расстояние между элементарными площадками
—
расстояние между элементарными площадками ![]() и
и ![]() ,
, ![]() и
и ![]() — углы
между нормалями к соответствующим элементарным площадкам и отрезком,
соединяющим эти площадки,
— углы
между нормалями к соответствующим элементарным площадкам и отрезком,
соединяющим эти площадки, ![]() равен 1, если
равен 1, если ![]() “видит”
“видит” ![]() и
0 в противном случае.
и
0 в противном случае.
Принимая во внимание, что ![]() и что в подавляющем большинстве случаев
и что в подавляющем большинстве случаев ![]() (если только фрагмент
(если только фрагмент![]() не оказался вогнутым), для сцены из n элементов требуется вычислить
по крайней мере
не оказался вогнутым), для сцены из n элементов требуется вычислить
по крайней мере ![]() коэффициентов формы.
коэффициентов формы.
Очевидно, что чем больше n, тем ближе решение соответствующей
системы к реальной функции излучательности. Однако выполнение ![]() весьма нетривиальных операций по вычислению матрицы коэффициентов формы
становится при больших n серьезной проблемой. Можно ли как-то
уменьшить объем вычислений?
весьма нетривиальных операций по вычислению матрицы коэффициентов формы
становится при больших n серьезной проблемой. Можно ли как-то
уменьшить объем вычислений?
Иерархическая излучательность. Вейвлет-излучательность
Развитием иерархического похода стало использование вейвлетов [1, 5, 6].
Метод основан на утверждении о том, что при проецировании интегрального
оператора уравнения излучательности на некоторое n-мерное
подпространство, в этом подпространстве можно так выбрать вейвлет-базис, что
для любого ![]() найдется такое
найдется такое ![]() ,
что все элементы полученной в результате проецирования матрицы, кроме
,
что все элементы полученной в результате проецирования матрицы, кроме ![]() или даже
или даже ![]() ,
не превысят (по модулю)
,
не превысят (по модулю) ![]() ,
и при замене этих элементов нулями в решение будет внесена ошибка, не
превосходящая
,
и при замене этих элементов нулями в решение будет внесена ошибка, не
превосходящая ![]() [4]. На содержательном уровне идея метода состоит в следующем. Для получения
удовлетворительного приближения решения часть коэффициентов формы можно
вычислить при достаточно грубом разбиении сцены на объекты — это касается
случая, когда размеры пар соответствующих фрагментов существенно меньше
расстояния между ними. В то же время для этих же самых фрагментов может
потребоваться дополнительное разбиение при вычислении коэффициентов формы в
паре с фрагментами, находящимися по соседству. Применение вейвлет-базиса
позволяет хранить как информацию, полученную при грубом разбиении, так и
уточняющую ее информацию.
[4]. На содержательном уровне идея метода состоит в следующем. Для получения
удовлетворительного приближения решения часть коэффициентов формы можно
вычислить при достаточно грубом разбиении сцены на объекты — это касается
случая, когда размеры пар соответствующих фрагментов существенно меньше
расстояния между ними. В то же время для этих же самых фрагментов может
потребоваться дополнительное разбиение при вычислении коэффициентов формы в
паре с фрагментами, находящимися по соседству. Применение вейвлет-базиса
позволяет хранить как информацию, полученную при грубом разбиении, так и
уточняющую ее информацию.
Построим начальное разбиение сцены так, чтобы каждый фрагмент этого разбиения легко параметризовался на единичном квадрате. В качестве вейвлет-базиса можно использовать как простейший вейвлет-базис Хаара [1, 6], так и более сложные конструкции вейвлетов [5].
Каждому фрагменту начального разбиения поставим в соответствие квадродерево. В начале все деревья имеют только корневые вершины. Вычисляется матрица коэффициентов формы для начального разбиения и находится решение (методом Гаусса-Зейделя). Все корневые вершины деревьев получают ссылку друг на друга. Ссылка соответствует вычисленному для соответствующей пары фрагментов коэффициенту формы. Далее попеременно выполняются шаги разбиения матрицы и вычисления модифицированной системы. Выполнение продолжается до тех пор, пока решение не будет удовлетворять заданной точности.
Критерий необходимости разбиения можно построить следующим образом: оценить перенос световой энергии, который имел бы место, если были бы вычислены новые коэффициенты формы. Если количество энергии не превосходит заданного порога, то соответствующие коэффициенты вычислять не стоит. Разбиение выполняется так: для каждого из уже посчитанных коэффициентов формы производится 1 шаг разбиения базисной функции, соответствующей либо фрагменту-“излучателю”, либо фрагменту-“приемнику”, либо им обоим, а к соответствующим вершинам деревьев добавляются вершины-потомки, потом выполняются оценки для всех возможных новых коэффициентов формы. Если какие-либо коэффициенты решено пересчитывать, то соответствующие ссылки на вершины деревьев переустанавливаются.
Немного иначе реализован метод в [6]. Сначала для исходного разбиения также строится лес деревьев. Далее для каждой пары фрагментов производится оценка погрешности вычисления коэффициента формы. Если ошибка ниже заданного порога, то коэффициент формы вычисляется и устанавливается соответствующая ссылка. Если нет, то происходит разбиение одного из фрагментов, соответствующая вершина получает потомков и снова выполняется процедура оценки. Промежуточных решений на этом этапе не ищется, решение ищется один раз по окончании процедуры вычисления коэффициентов формы (и формирования деревьев).
Литература