Начало: 14 апреля 2004
Конец: 28 апреля 2004 (23:59)
Автор задания:
Евгений Лисицин
Введение
Цель задания - получение навыков работы с геометрическими
объектами в двух- и трехмерном пространствах, понятия о
морфировании геометрических объектов, навыков простейшей визуализации
данных с помощью OpenGL.
Требуется создать программу, позволяющую осуществлять
морфирование двух- и трехмерных объектов определенной формы.


Рис.1 Примеры морфирования в двух- и трехмерном
пространствах.
Вы можете скачать пример
реализации задания в трехмерном пространстве.
Предлагаемый алгоритм
Мы приведем возможную реализацию для плоских выпуклых фигур. Алгоритм очевидно
обобщается для случая трехмерных фигур.
Подробное описание алгоритма можно найти в прилагаемой к заданию
статье.
Рассмотрим процесс морфирования выпуклой Фигуры А в выпуклую Фигуру B.
Пусть морфинг производится в течение промежутка времени [0,1]. Необходимо
указать для каждого момента времени t из [0,1]
фигуру AB(t) такую, что AB(0) = A,
AB(1) = B, причем изменение AB с течением
времени - плавное.
Этап I. Создание описывающих фигур.
Через грани фигуры А проводятся прямые - назовем их
ограничивающими прямыми. Фигура, ограничиваемая этими прямыми - A''.
Производится параллельный перенос ограничивающих прямых таким образом, чтобы
A'' была минимальной фигурой, содержащей фигуру B
(Рис. 2). Параллельный перенос граней по отдельности показан на Рис.2a, 2b, 2c.
На Рис. 2d показан результат: исходная фигура "описала" конечную. Если
производить перенос в течение конечного промежутка времени, получим морфинг
А в А'':
A' = A'(t)
A'(0) = A
A'(1) = A''
Аналогно создается образ B'' фигуры B,
содержащий фигуру А, и морфинг B' = B'(t).
Построение образа показано на Рис. 3a-d.
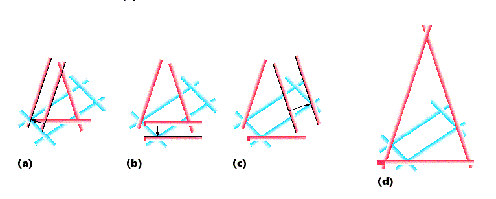
Рис.2 Создание описывающих фигур.
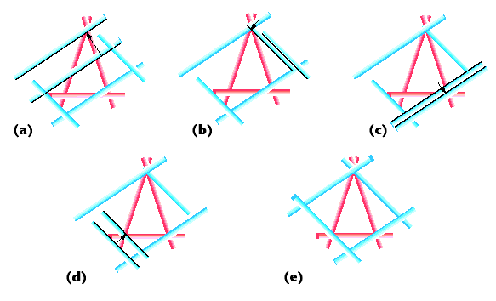
Рис.3 Создание описывающих фигур.
Этап II. Морфирование.
Для того, чтобы построить непрерывное морфирование фигур A и
B друг в друга, одновременно производится морфинг A
в A' и B' в B. Для каждого
t из [0,1] строится фигура AB'(t),
являющаяся пересечением A'(t) и B'(t).
Процесс получения промежуточных фигур показан на Рис. 4а. Результат
показан на Риc. 4b.
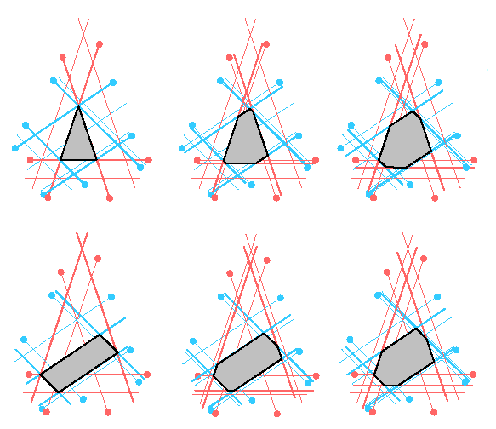
Рис.4а Процесс морфинга.

Рис.4b Процесс морфинга.
Заметим, что:
AB'(0) = A
AB'(1) = B
AB изменяется плавно с течением времени
Таким образом, AB'(t) - морфинг между фигурами A
и B.
Подробное описание алгоритма для трехмерного случая
Примечание: людям, желающим поупражнять ум линейной алгеброй,
рекомендуется пропустить этот раздел. Для остальных подробно описывается, как
решать задачу.
Шаг 1. Построение описывающих фигур.
Предположим, что нормали граней фигуры А направлены наружу, будем
называть полупространство относительно грани (или плоскости, содержащей грань)
фигуры А положительным ( P+(a) ), если
нормаль грани направлена в это полупространство.
Зададимся разрешением морфинга (количеством промежуточных фигур между A
и B) - N.
-
Возьмем грань фигуры А , обозначим плоскость, ее содержащую, a.
Вычислим минимальный вектор d, такой что фигуры А и
B будут целиком лежать по одну сторону от грани a',
полученной из a путем сдвига на d.
-
Среди всех вершин фигуры В найдем вершину M, наиболее
удаленную от плоскости a и находящуюся в P+(a) .
Проекция вектора из произвольной точки a в M на нормаль a будет
искомым вектором d.
-
Обозначим плоскость, полученную из a путем добавления к ней d*(i/N)
, как a(i).
-
Повторим шаг 1 для всех граней фигур А. Множество полученных
граней для каждого i обозначим A(i).
Для фигуры B повторим ту же самую процедуру, за
исключением: обозначение b(i) для граней фигуры B будет
означать b + d*(N-i/N) .
Шаг 2. Генерация морфинга.
Для получения i-го шага морфинга необходимо найти фигуру,
ограничиваемую множествами плоскостей A(i) и B(i).
Объединение этих множеств назовем C(i) .
-
Найдем множество Q' точек, где пересекаются три или более
граней из С(i).
-
Получем из Q' множество Q путем отбрасывания
точек, находящихся в положительном полупространстве хотя бы одной из плоскостей
из C(i).
-
Сформируем грани промежуточной фигуры из точек Q.
-
Для каждой плоскости из C(i) найдем точки из Q,
принадлежащие ей (расстояние от плоскости до точки равно нулю). Эти точки
станут вершинами грани.
-
Занумеруем точки так, чтобы они образовали выпуклый многоугольник. Выберем
вектор b, соединяющий две произвольно выбранные точки
A и B из
рассматриваемого набора. Обозначим n - нормаль к плоскости, которой принадлежат
точки набора (плоскость можно найти по любым трем точкам набора).
Нумерацию точек набора проведем в соответствии с углом, на который нужно
повернуть b вокруг A, чтобы плоскость,
проходящая через n и q, включила отличную
от A и B точку С из набора, т.е. между векторами b
и c = AC. Примечание: при нумерации имейте в виду, что потом вам
понадобится найти нормаль полученной грани.
Примечание: решаемая на этапе 3 задача - суть нахождение выпулой
оболочки для множества точек Q. Существуют более изящные
алгоритмы решения этой задачи. Реализация подобных алгоритмов - повод для
получения бонуса.
Обязательная часть
Обязательная часть предполагает реализацию морфирования выпуклых
многоугольников в двумерном пространстве. В программе есть жестко определенные
начальный и конечный многоугольники. По команде пользователя запускается
процесс морфирования.
Процесс морфирования должен быть хорошо виден на экране -
скорость процесса должна быть разумной.
Исходная и конечная фигуры должны существенно отличаться: разное
количество вершин, ребер и т.п.
Вместо плоских фигур (или дополнительно к ним) можно реализовать морфирование в трехмерном
пространстве - за этот вариант дается большее количество баллов. Визуализация
процесса производится с применением библиотеки OpenGL.
Дополнительная часть
Ниже приведены возможности, за реализацию которых можно получить
дополнительные баллы.
-
Управление ходом морфирования: кнопки вперед, назад,
приостановить, сделать один шаг морфирования.
-
Считывание моделей многоугольников или многогранников из файла.
Формат файла для двумерного случая:
В каждой строке хранится разделенные пробелом координаты вершин. Номер вершины совпадает с номером
строки. Вершины нумеруется по часовой стрелке. Координаты вершины -
действительные числа, находятся в диапазоне [-1,1]. ,
Формат файла для трехмерного случая:
MESH_FILE ::=
{
MESH_VERTEX_LIST { < VERTEX_LIST > }
MESH_FACE_LIST { < FACE_LIST > }
}
VERTEX_LIST ::= < VERTEX_DEF > | < VERTEX_LIST>, < VERTEX_DEF >
FACE_LIST ::= < FACE_DEF > | < FACE_LIST>, < FACE_DEF >
VERTEX_DEF ::= < DOUBLE > < DOUBLE > < DOUBLE >
FACE_DEF ::= < INT > | < FACE_DEF > < INT >
Примечание: в описании символ { и лексемы MESH_VERTEX_LIST, MESH_FACE_LIST
нужно рассматривать как строковые константы. - целое неотрицательное число,
- вещественное число в диапазоне [-1,1].
-
Блендинг цвета или текстуры. Блендинг цвета - постепенное изменение
цвета в процессе морфирования одной фигуры в другую. Блендинг текстуры: на
исходную и целевую модели многогранников накладываются текстуры. Текстура промежуточных
моделей морфинга представляет из себя смесь текстур исходной и конечной моделей,
полученную средствами мультитекстурирования OpenGL (см. Материалы для выполнения задания).
Примеры моделей многоугольников и многогранников:
Материалы для выполнения задания
Предлагается реализовать морфирование, описанное в статье
DMorph by Andrew Glasser
Для изучения возможностей OpenGL предлагаются следующие
материалы
Стандартная библиотека GL и библиотека GLU, как правило, входит
в поставку среды программирования. Библиотеку GLUT (версия для Microsoft Visual
C++) можно скачать
здесь.
При реализации задания можно пользоваться библиотекой
GML.
Требования к программе
Обязательное требование - выполнить обязательную часть задания.
При этом программа должна работать в интерактивном режиме, т.е. количество
кадров в секунду не должно опускаться ниже 5-10 на современной машине с
ускорителем графики.
Еще одно обязательное требование - разбираться в материале. В
спорных ситуациях оценка выставляется после личной беседы, выявляющей понимание
принципа действия основных алгоритмов.
К программе должны прилагаться все необходимые для ее запуска
библиотеки. (опускать можно только слишком большие библиотеки, если они явлются
стандартными). Отсутствие библиотек создает неудобства при проверке, однако не
фатально. У нас есть набор из наиболее часто недостающих библиотек для Borland
C++ Builder и MS Visual C++.
Примечание: glut32.dll в архив можно не включать.
Оценка
| Двумерное морфирование |
4 балла
|
| Проверка выпуклости: |
2 балла |
| Трехмерное морфирование |
8 баллов
|
| Управление морфированием |
1-3 балла
|
| Навигация мышкой (вращение модели) |
1 балл
|
| Блендинг цвета |
2 балла |
| Блендинг текстуры |
3 балла |
| Загрузка из файла (двумерный
вариант): |
2 балла
|
| Загрузка из файла (трехмерный
вариант): |
4 балла |
Оформление не отличается от обычного.
ZIP-архив с исходными текстами и исполняемыми файлами, названный
по схеме GZV_nnnnnnnn.zip (где G - последняя цифра номера группы, Z - номер задания, V - номер версии задания, nnnnnnnn
- номер студенческого билета) присылайте на assign4@graphics.cs.msu.su
Например, студент 206 группы с номером студенческого билета 06529042, сдающий обновленную (вторую) версию программы по
второму заданию, должен прислать архив с именем 622_06529042.zip.
Также смотрите здесь, какие
файлы нам присылать и как их оформить Советуем очень внимательно
прочитать весь FAQ
Не забудьте положить в архив файл readme.txt. В файле описать интерфейс програмы (алгоритм
работы с программой, пункты меню, управляющие клавиши)
Результаты смотрите в интернете и/или на стенде около комнаты 703.
Примечания
- Задание выполняется строго индивидуально. За совместную работу
или обмен кусками кода ставится -5 баллов всем участникам,
если факт командной работы не был указан в readme.txt заданий.
- Рекомендуется написание программы под семейство ОС Windows.
Написание под другие операционные системы нежелательно и может
вызвать задержки с проверкой таких работ.
|
