|
Реализовать клеточный автомат
Клеточные автоматы являются
дискретными динамическими системами, поведение которых полностью определяется
в терминах локальных взаимозависимостей их состояний. Клеточный автомат представляет собой
равномерную n-мерную сетку (конечную или бесконечную), каждая ячейка (клетка)
которой может принимать состояние из некоторого набора состояний; время идет дискретными шагами,
а законы развития (изменения состояний клеток) выражаются единственным набором правил, например небольшой
справочной таблицей, по которой любая клетка на каждом шаге вычисляет свое
новое состояние по состояниям ее близких соседей. Если задан подходящий
набор правил, то такой простой операционный механизм достаточен для поддержания
целой иерархии структур и явлений. Клеточные автоматы дают полезные модели
для многих исследований в естественных науках. Они образуют общую парадигму
параллельных вычислений, подобно тому, как это делают машины Тьюринга для
последовательных вычислений.
Хорошим примером для ознакомления
с принципами работы клеточного автомата является игра Джона Хортона Конвея
"Жизнь".
Общие правила построения
клеточных автоматов можно сформулировать следующим образом:
-
Состояние клеток дискретно (обычно
0 и 1, хотя могут быть автоматы и с большим числом состояний).
-
Соседями являются ограниченное
число клеток, часто это ближайшие клетки.
-
Правила, задающие динамику развития
клеточного автомата, обычно имеют простую функциональную форму и зависят
от решаемой проблемы.
-
Клеточный автомат является тактируемой
системой, т.е. смена состояний клеток происходит одновременно.
Клеточные автоматы предоставляют
большую свободу в выборе структуры и правил развития системы. Это позволяет
моделировать на их основе или решать с их помощью
самые разнообразные задачи:
-
моделирование химических и физических
процессов,
-
проведение исследований по "Искусственной
жизни" (Artificial Life)
-
исследование биологических процессов
-
моделирование распространения
слухов
(http://www.island-formoza.ru/tech_bred/index.html)
-
и т.д.
Клеточные автоматы различаются,
в частности, количеством состояний клеток, размерностью сетки и правилом
изменения состояний клеток. Мы рассмотрим некоторые разновидности автоматов
с двумерной сеткой.
В двумерных автоматах соседями
клеток обычно считаются 5 клеток - сама клетка и 4 ее непосредственных
не диагональных соседа (окрестность фон Неймана), или 9 клеток - сама клетка и 8 ее непосредственных
соседей, включая диагональные клетки (окрестность Мура).
Состояние клеточного автомата
может быть описано матрицей, например:
Здесь состояния клеток записываются
в соответствующих ячейках матрицы.
Но намного интереснее
представить состояние в виде изображения, где каждый пиксел соответствует
клетке, и текущий цвет пиксела определяется состоянием клетки.
- Автоматы серии "Поколения"
Автоматы с числом состояний
более чем два.
Правила изменений состояния
клетки записываются следующим образом
S/B/C
где:
S - набор цифр от 0 до 8,
определяет
число "живых" соседей, при котором клетка остается "в живых",
B - набор цифр от 0 до 8,
определяет
число "живых" соседей при котором "мертвая" клетка становится "живой"
С - число, определяет число
ходов "умирания" клетки
Например - 23/3/14
Означает, что клетка живет,
если у нее 2 или 3 соседа,
что при ровно трех соседях
"рождается" новая клетка, и
что клетка умирает за четырнадцать
ходов.
Если число "живых" соседей
у клетки не равняется ни одной из цифр из набора S, клетка
начинает "умирать" и ее состояние увеличивается с каждым ходом, пока не
достигнет C, после чего клетка пропадает.
"Умирающая" клетка не участвует в подсчете числа "живых" соседей при расчете
следующего шага. При рождении клетка получает первое состояние ("клетка жива").
"Искры"
2/2/25
На рисунке представлены 0-ая, 16-ая, 32-ая, 48-ая, 64-ая и 80-ая конфигурациии:
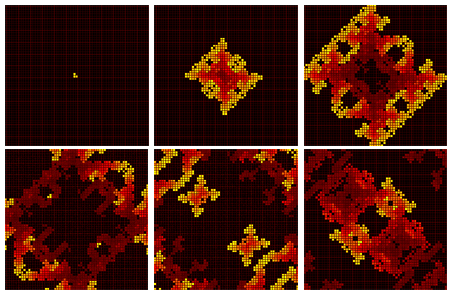
"Букашки"
23/2/8
На рисунке представлены 0-ая, 16-ая, 32-ая, 48-ая, 64-ая и 80-ая конфигурациии
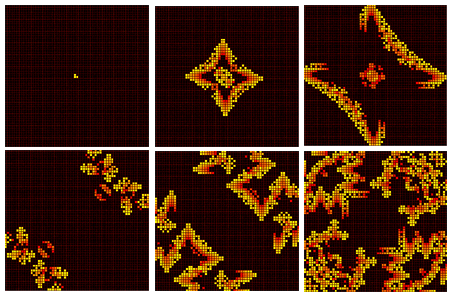
"Пламя"
235678/3468/9
На рисунке представлены 0-ая, 16-ая, 32-ая, 48-ая, 64-ая и 80-ая конфигурациии
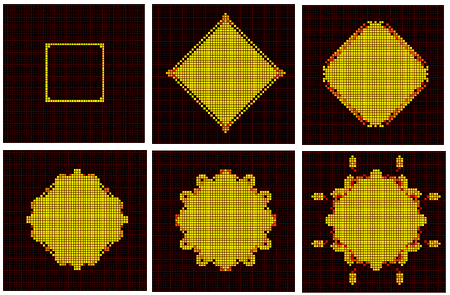
- Автомат "Клеточная вселенная"
Еще один пример клеточного автомата, открытый Дейвидом Гриффитом
из Висконсинского университета в Мэдисоне. Стартуя из произвольно выбранного исходного состояния, автомат демонстрирует
четыре различные фазы, завершающиеся причудливыми кристаллическими образованиями, сильно напоминающими примитивные формы жизни.
Правило поведения автомата заключается в том, чтобы пронумеровать возможные состояния
от 0 до n - 1 и считать, что если клетка находится на данном такте в состоянии k, то на следующем такте она должна "съесть"
любые соседние клетки, находящиеся в состоянии k - 1. Съедение проявляется в том, что съеденная соседняя клетка переходит
из состояния k - 1 в состояние k; клетка в состоянии 0 может поедать соседние клетки в состоянии n - 1.
На рисунке представлен пример реализации такого автомата (поле 80х80, n=17). Каждый фрагмент на 12 итераций отличается от предыдущего.

- Автоматы серии "Тьюрмиты"
Тьюрмит - это некий синтез клеточного автомата и машины Тьюринга. От клеточного автомата тьюрмит отличается тем, что в начальный
момент времени его поле пусто и какая-то одна клетка считается начальной (тьюрмит занимает начальную позицию, находится
в начальном состоянии, начальное направление, например, на восток). Затем на каждом такте применяется правило вида:
<текущее состояние><старый цвет текущей клетки><новый цвет><направление перемещения><новое состояние>
Состояния принято обозначать латинскими буквами; цвета - числами от 0 до 15 (16-ти цветовая палитра), причем начальный цвет
черный (это не жесткое ограничение, при желании цветовую гамму можно обогатить и придумать свои обозначения); направление
перемещения изменяется относительно текущего курса тьюрмита, обозначается числами -1 (повернуть налево), 1 (повернуть направо),
0 (прямо).
Например, правило А 0 15 0 В означает, что если тьюрмит находится в состоянии А и стоит на черной клетке, то он должен покрасить
ее в белый цвет, продвинуться на одну клетку в текущем направлении и перейти в состояние В.
Таким образом, если А - начальное состояние тьюрмита, 0 - начальный цвет, то набор правил тьюрмита должен содержать
правило А 0 _ _ _.
"Кактус"
(на рисунке представлена одна из возможных конфигураций)
 |
Система правил:
A 0 2 1 A
A 2 10 -1 B
A 10 0 -1 B
B 0 2 1 A
B 2 2 -1 A
B 10 2 -1 A |
"Спираль Тэрка"
(на рисунке представлена одна из возможных конфигураций)
 |
Система правил:
A 0 2 -1 A
A 2 0 0 B
B 0 2 1 A
B 2 2 1 A |
"Нить Ариадны:"
(на рисунке представлена одна из возможных конфигураций)
 |
Система правил:
A 0 15 0 D
A 15 0 0 B
E 0 15 0 C
E 15 15 0 B
B 0 0 -1 E
B 5 5 1 A
B 15 15 1 E
B 1 1 1 E
C 0 15 -1 E
C 15 1 -1 A
C 1 5 -1 A
C 5 0 -1 A
D 0 5 -1 A
D 5 15 -1 A
D 15 1 -1 A
D 1 0 -1 A |
"Спираль:"
(на рисунке представлена одна из возможных конфигураций)
 |
Система правил:
A 0 15 0 D
A 15 0 0 B
E 0 15 0 D
E 15 15 0 B
B 0 0 1 E
B 1 1 1 E
B 5 5 1 A
B 15 15 1 E
C 0 15 -1 A
C 15 1 -1 A
C 1 5 -1 A
C 5 0 -1 A
D 0 5 -1 A
D 5 15 -1 A
D 15 1 -1 A
D 1 0 -1 A |
Программа
должна выводить на экран монохромное или цветное изображение состояния одного из предложенных
автоматов. Необходимо, чтобы
сетка автомата была достаточно велика, как минимум 200х200 клеток. Программа должна
показывать эволюцию автомата. Также нужно реализовать возможность вручную задавать
начальную конфигурацию автомата, или предоставить набор нескольких начальных состояний.
| Реализация одного автомата (требуемый минимум) |
6 баллов |
| Реализация нескольких однотипных автоматов (поколения, тьюрмиты) |
+1 балл |
| Реализация нескольких автоматов разных типов (не менее трех) |
+2 балла |
Удобная реализация возможности редактирования начального состояния автомата. |
+2 балла |
| Быстрый расчет
(оптимизировать скорость), удачный интерфейс |
+1, +2 балла |
Оформление не отличается от обычного.
ZIP-архив с исходными текстами и исполняемыми файлами, названный
по схеме GZV_nnnnnnnn.zip (где G - последняя цифра номера группы, Z - номер задания, V - номер версии задания, nnnnnnnn
- номер студенческого билета) присылайте на assign1@graphics.cs.msu.su
Например, студент 206 группы с номером студенческого билета 06529042, сдающий обновленную (вторую) версию программы по
первому заданию, должен прислать архив с именем 612_06529042.zip.
Также смотрите здесь, какие
файлы нам присылать и как их оформить Советуем очень внимательно
прочитать весь FAQ
Не забудьте положить в архив файл readme.txt. В файле описать интерфейс програмы (алгоритм
работы с программой, пункты меню, управляющие клавиши) и указать следующие
подзадания:
Реализация автомата: [указать реализованный автомат(ы)]
Возможность редактирования начального состояния автомата: [+/-]
Работа с программой: [алгоритм работы с программой]
Результаты смотрите в интернете и/или на стенде около комнаты 703
Все вопросы присылать авторам
и проверяющим .
Примечания
- Задание выполняется строго индивидуально. За совместную работу
или обмен кусками кода ставится ноль баллов всем участникам,
если факт командной работы не был указан в readme.txt заданий.
- Рекомендуется написание программы под семейство ОС Windows.
Написание под другие операционные системы нежелательно и может
вызвать задержки с проверкой таких работ.
Где можно найти подробные материалы по программированию под Windows?
Например, на сайте http://www.firststeps.ru.
В задании в разделе "поколения" сказано, что при определенном числе соседей мертвая клетка
становится живой. Оживает ли умирающая клетка (в подсчете числа живых она не участвует)?
Нет, умирающая клетка не считается мертвой, поэтому стать живой не может.
Что значит "тьюрмит поворачивает налево/направо"?
Допустим, тьюрмит движется на восток.
На картинке темно-серым цветом обозначено, где тьюрмит
был на предыдущем такте, красным - текущее положение тьюрмита, а светло-серым - где он окажется на следующем такте
при движении налево (верхний вариант), направо (нижний вариант)
или прямо (средний вариант).
В разделе "Поколения" в какой момент мы обозначаем клетку "умирающей": после
того, как мы посчитали новое состояние автомата (в предыдущем она не умирала) или сразу же как только мы
посчитали, что число соседей у нее такое, что она должна уже умирать?
Сразу же, как только у клетки появилось неположенное число соседей, она начинает умирать. Не должно быть состояния
автомата, при котором у живой клетки число соседей не совпадает ни с одним из набора S.
|
