|
Начало: 3 мая 2003
Конец: 17 мая 2003 (23:59)
Автор задания:
Александр Мальковский
Введение
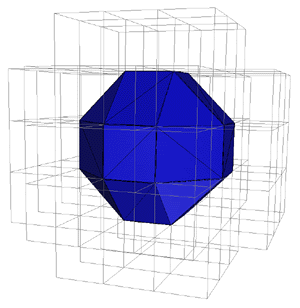
Цель задания - визуализация изоповерхности скалярного поля, заданного с помощью точечного потенциала расположенного в трехмерном пространстве.
Описание задания
Часто в компьютерной графике приходится сталкиваться с
визуализацией элементов существующих абстрактно, с визуальной точки зрения, но
реально не видимых. Форма и атрибуты таких элементов задаются посредством не
геометрических абстракций, а основываясь на других предметных областях,
например, на физических или биологических свойствах отображаемого объекта.
Технология Marching Cubes была
разработана с целью визуализации изоповерхностей посредством трехмерных
скалярных полей. Также в методе обеспечивается высокая скорость и качество
визуализации, что позволяет использовать подобные методы в приложения реального
времени.
Предполагается, что пространство представимо в виде
трехмерной сетки, то есть представляет из себя набор набор вокселей, которые
являются минимальными структурными единицами этого пространства.
Предположим, нам необходимо визуализировать скалярные поля,
задающиеся с помощью точечного потенциала расположенного в трехмерном
пространстве. Каждый отдельный потенциал представляет из себя шар с убыванием
потенциала от центра к границе. Убывание потенциала может
происходит, например, по следующему закону:
C(r) = a(r6 / R6)
+ b(r4 / R4) + c(r2 / R2) + 1,
где а = -0.444444,
b = 1.888889,
c = -2.444444
Однако, в местах где области
действия отдельных потенциалов пересекаются, результирующее поле теряет
шароподобную структуру и имеет форму "склеивающихся капель", то есть область
соприкасания имеет гладкую структуру.
Нам необходимо визуализировать скалярное поле соответствующее некоторому
значению потенциала. Соответственно, так как минимальной единицей нашего
пространства являются воксели (имеющие форму куба или, в общем случае,
параллелипипида), то нам необходимо выбрать все воксели лежащие на границе
заданного значения потенциала и отобразить их в соответствии с распределением
потенциала внутри них. Конкретизируя все выше сказанное, выбирается воксель, для
которого необходимое значение является средним, то есть для части вершин
выполняется неравенство превосходства, а для части оно неверно.
Существуют два основных метода по построению результирующей изоповерхности в
зависимости от распределения потенциала внутри вокселя: метод
Wyvill и метод Lorensen.
Метод Wyvill
Данный метод работает с
гранями вокселя, то есть не рассматривает воксель как трехмерную структуру. Для
каждой грани строится набор отрезков в зависимости от распределения потенциала
на этой грани (то есть от вершин, где значения потенциала больше либо равно
заданному и от вершин где значение потенциала меньше заданного).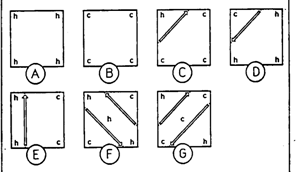
for
each edge of cube, <p,q> do
if
p is hot and q is cold or p is cold and q is hot
then
create intersection <p,q>;
for
each face of cube do create edges according to Fig. below;
while
edges remain do
begin
start := any edge;
poligon:=[start];
remove
start from age array;
next:=successor of start;
while
next <> start do
begin
polygon:=polygon+[next];
remove next
from edge array
end;
output
polygon
end
Выше приведен алгоритм
построения изоповерхности методом Wyvill.
Заметим, что в случаях F и
G возникает неоднозначность построения, если
основываться только на значениях потенциала в вершинах. Для устранения
неоднозначности производится дополнительное вычисление потенциала в центре грани,
и уже на основании центрального значения принимается
решение о правильном построении изоповерхности.
Стоит отметить, что на практике данный метод
применяется достаточно редко ввиду того что он работает не с трехмерными
объектами и нам приходится проводить корректное склеивание полученных отрезков в
целую грань, что является нежелательным в приложениях реального времени, так как
мы не получаем готовых примитивов, с которыми можно работать напрямую с
графическим процессором. Также затруднительными становятся различные оптимизации,
связанные с архитектурой и особенностями графических процессоров. Более под все
эти условия подходит метод Lorensen.
Метод Lorensen
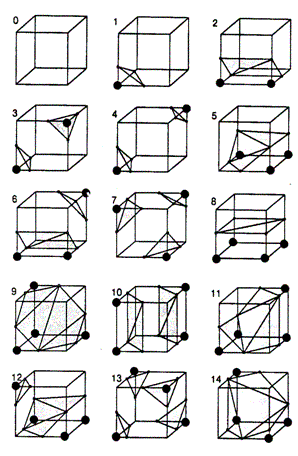
Данный метод рассматривает все возможные комбинации точек со
значением "больше" и со значением "меньше" заданного. С учетом симметрии
Lorensen предложил, что различных возможных
комбинаций всего 15 (хотя варианты 11 и 14 все-таки симметричны). Понятно, что
всего различных комбинаций существует 2^8=256.
Таким образом, по набору вершин с "большими" и "меньшими"
значениями" (множество которых ограничено 256 значениями) мы заранее знаем набор
примитивов (в данном случае, треугольников) которые будут его отображать.
Следовательно мы можем заранее просчитать эти примитивы, а также их аттрибуты (нормали,
цвета, и т.д).
Как и в предыдущем методе, в некоторых случаях возможна
неоднозначность в построении изоповерхности. В методе
Lorensen эту проблему сложно разрешить методом,
который использовался при аналогичных проблемах в методе
Wyvill. Поэтому в качестве решения принимают только один из возможных
вариантов. Таким образом возникновения "дырок" в изоповерхности не будет, но
возможна некоторая структурная нерегулярность при отдельных положениях камеры.
Данный метод широко используется при построении изоповерхностей,
и в дальнейшем мы будем рассматривать именно его.
Реализация.
Для применения метода Lorensen сначала
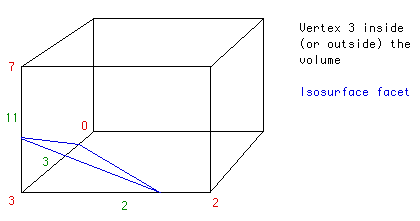
пронумеруем все вершины и ребра вокселя в определенном порядке, например, как
предолжено на рисунке. В дальнейшем мы будем основываться именно на этой
структуре.
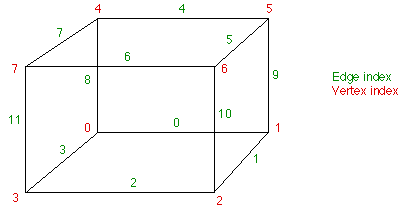
Пусть, например, значение потенциала в вершине 3 меньше
заданного, а во всех остальных вершинах - больше. Следовательно результирующая
изоповерхность должна проходить через грани 2, 3, 11. Точные положения вершин на
ребрах зависят от разностей потенциалов на граничных точках ребра и требуемого
значения. В данном случае - от 3-2, 3-0 и 3-7.
Понятно, что большой набор возможных комбинаций (256) ставит
задачу продуманной работы с такими большими массивами данных без потери
производительности и с достаточной степенью гибкости для возможности дяльнейших
оптимизаций. Для этого было предложено ряд решений, рассмотреных ниже.
Для начало, основываясь на принятой нами индексации вершин,
составляется идентификатор комбинации, который может принимать значение от 0 до
255 (по числу возможных вариантов). Считается он следующим образом:
cube_index
= 0;
if (grid.val[0] < isolevel) cube_index |= 1;
if (grid.val[1] < isolevel) cube_index |= 2;
if (grid.val[2] < isolevel) cube_index |= 4;
if (grid.val[3] < isolevel) cube_index |= 8;
if (grid.val[4] < isolevel) cube_index |= 16;
if (grid.val[5] < isolevel) cube_index |= 32;
if (grid.val[6] < isolevel) cube_index |= 64;
if (grid.val[7] < isolevel) cube_index |= 128;
Далее строится таблица, которая для
каждого индекса, подсчитанного указанным выше способом, определяет те ребра,
которые будет пересекать изоповерхность. Так как ребер всего 12, то данная
таблица содержит 12-битные числа, подсчитанные аналогичным способом, как и
cubeindex. Данную таблицу необходимо использовать
для того, чтобы определить позицию точки треугольника из изоповерхности
на ребре. Возможный вариант такой таблицы приведен ниже:
int edge_table[256]
=
{
0x0 , 0x109, 0x203, 0x30a, 0x406, 0x50f, 0x605, 0x70c,
0x80c, 0x905, 0xa0f, 0xb06, 0xc0a, 0xd03, 0xe09, 0xf00,
0x190, 0x99 , 0x393, 0x29a, 0x596, 0x49f, 0x795, 0x69c,
0x99c, 0x895, 0xb9f, 0xa96, 0xd9a, 0xc93, 0xf99, 0xe90,
0x230, 0x339, 0x33 , 0x13a, 0x636, 0x73f, 0x435, 0x53c,
0xa3c, 0xb35, 0x83f, 0x936, 0xe3a, 0xf33, 0xc39, 0xd30,
0x3a0, 0x2a9, 0x1a3, 0xaa , 0x7a6, 0x6af, 0x5a5, 0x4ac,
0xbac, 0xaa5, 0x9af, 0x8a6, 0xfaa, 0xea3, 0xda9, 0xca0,
0x460, 0x569, 0x663, 0x76a, 0x66 , 0x16f, 0x265, 0x36c,
0xc6c, 0xd65, 0xe6f, 0xf66, 0x86a, 0x963, 0xa69, 0xb60,
0x5f0, 0x4f9, 0x7f3, 0x6fa, 0x1f6, 0xff , 0x3f5, 0x2fc,
0xdfc, 0xcf5, 0xfff, 0xef6, 0x9fa, 0x8f3, 0xbf9, 0xaf0,
0x650, 0x759, 0x453, 0x55a, 0x256, 0x35f, 0x55 , 0x15c,
0xe5c, 0xf55, 0xc5f, 0xd56, 0xa5a, 0xb53, 0x859, 0x950,
0x7c0, 0x6c9, 0x5c3, 0x4ca, 0x3c6, 0x2cf, 0x1c5, 0xcc ,
0xfcc, 0xec5, 0xdcf, 0xcc6, 0xbca, 0xac3, 0x9c9, 0x8c0,
0x8c0, 0x9c9, 0xac3, 0xbca, 0xcc6, 0xdcf, 0xec5, 0xfcc,
0xcc , 0x1c5, 0x2cf, 0x3c6, 0x4ca, 0x5c3, 0x6c9, 0x7c0,
0x950, 0x859, 0xb53, 0xa5a, 0xd56, 0xc5f, 0xf55, 0xe5c,
0x15c, 0x55 , 0x35f, 0x256, 0x55a, 0x453, 0x759, 0x650,
0xaf0, 0xbf9, 0x8f3, 0x9fa, 0xef6, 0xfff, 0xcf5, 0xdfc,
0x2fc, 0x3f5, 0xff , 0x1f6, 0x6fa, 0x7f3, 0x4f9, 0x5f0,
0xb60, 0xa69, 0x963, 0x86a, 0xf66, 0xe6f, 0xd65, 0xc6c,
0x36c, 0x265, 0x16f, 0x66 , 0x76a, 0x663, 0x569, 0x460,
0xca0, 0xda9, 0xea3, 0xfaa, 0x8a6, 0x9af, 0xaa5, 0xbac,
0x4ac, 0x5a5, 0x6af, 0x7a6, 0xaa , 0x1a3, 0x2a9, 0x3a0,
0xd30, 0xc39, 0xf33, 0xe3a, 0x936, 0x83f, 0xb35, 0xa3c,
0x53c, 0x435, 0x73f, 0x636, 0x13a, 0x33 , 0x339, 0x230,
0xe90, 0xf99, 0xc93, 0xd9a, 0xa96, 0xb9f, 0x895, 0x99c,
0x69c, 0x795, 0x49f, 0x596, 0x29a, 0x393, 0x99 , 0x190,
0xf00, 0xe09, 0xd03, 0xc0a, 0xb06, 0xa0f, 0x905, 0x80c,
0x70c, 0x605, 0x50f, 0x406, 0x30a, 0x203, 0x109, 0x0
};
Работа с такой таблицей производится следующим образом:
Vector
vert_list[12]; // array of points of result surface
// Cube is
entirely in/out of the surface
if (edge_table[cube_index]
== 0)
return false;
// Find the vertices where the surface intersects
the cube
if (edge_table[cube_index]
& 1)
vert_list[0] = VertexInterp(isolevel,
grid.p[0], grid.p[1],
grid.val[0], grid.val[1]);
if (edge_table[cube_index]
& 2)
vert_list[1] = VertexInterp(isolevel,
grid.p[1], grid.p[2],
grid.val[1], grid.val[2]);
if (edge_table[cube_index]
& 4)
vert_list[2] = VertexInterp(isolevel,
grid.p[2], grid.p[3],
grid.val[2], grid.val[3]);
if (edge_table[cube_index]
& 8)
vert_list[3] = VertexInterp(isolevel,
grid.p[3], grid.p[0],
grid.val[3], grid.val[0]);
if (edge_table[cube_index]
& 16)
vert_list[4] = VertexInterp(isolevel,
grid.p[4], grid.p[5],
grid.val[4], grid.val[5]);
if (edge_table[cube_index]
& 32)
vert_list[5] = VertexInterp(isolevel,
grid.p[5], grid.p[6],
grid.val[5], grid.val[6]);
if (edge_table[cube_index]
& 64)
vert_list[6] =
VertexInterp(isolevel, grid.p[6],
grid.p[7], grid.val[6],
grid.val[7]);
if (edge_table[cube_index]
& 128)
vert_list[7] = VertexInterp(isolevel,
grid.p[7], grid.p[4],
grid.val[7], grid.val[4]);
if (edge_table[cube_index]
& 256)
vert_list[8] = VertexInterp(isolevel,
grid.p[0], grid.p[4],
grid.val[0], grid.val[4]);
if (edge_table[cube_index]
& 512)
vert_list[9] = VertexInterp(isolevel,
grid.p[1], grid.p[5],
grid.val[1], grid.val[5]);
if (edge_table[cube_index]
& 1024)
vert_list[10] = VertexInterp(isolevel,
grid.p[2], grid.p[6],
grid.val[2], grid.val[6]);
if (edge_table[cube_index]
& 2048)
vert_list[11] = VertexInterp(isolevel,
grid.p[3], grid.p[7],
grid.val[3], grid.val[7]);
Здесь VertexInterp(...) -
функция осуществляющая вычисление расположения
точки, являющейся точкой ребра примитива изоповерхности, на ребре посредством
интерполяции. Как уже говорилось выше, позиция точки зависит от значений
потенциала в вершинах и искомого значения потенциала. Пусть
P1, P2 - координаты граничных точек ребра,
V1, V2 - величины потенциала в этих
точках соответственно, isovalue - искомое
значение потенциала. Тогда точка пересечения ребра и изоповерхности вычисляется
следующим образом:
P = P1 + (isovalue - V1)
(P2 - P1) / (V2 - V1)
Заметим, что если не проводить интерполяцию, а использовать за
искомое значение, например, середину ребра, то все возможные треугольники могут
быть просчитаны заранее, и, как следствие, могут быть просчитаны заранее нормали
и другие атрибуты для них, следовательно мы избавляемся от большой работы,
которую нам иначе бы пришлось выполнять в реальном времени.
Однако, приходится мириться с потерей качества. Следовательно, в приложениях,
где требуется высокая точность построения, необходимо проводить интерполяцию, а
в приложениях, где построение изоповерхности используется лишь как
дополнительный элемент визуализации, достаточно грубого, но быстрого построения
изоповерхности с полным предвычислением геометрии.
В завершении нам необходимо собрать все построенные треугольники
и вывести их на экран. Для этого используется следующая таблица, индексируемая
по cube_index и содержащая для каждого из 256
случаев набор треугольников, получаемый в результате пересечения изоповерхности
и вокселя. Пример такой таблицы (tri_table)
можно найти здесь. Тогда получение результирующих
треугольников, задающих изоповерхность в данном вокселе сводится к следуещей
процедуре:
// Create the triangles
int ntrgs = 0;
for (i = 0;
tri_table[cube_index][i]
!= -1; i
+= 3)
{
trgs[ntrgs].v[0]
= vert_list[tri_table[cube_index][i]];
trgs[ntrgs].v[1]
= vert_list[tri_table[cube_index][i+1]];
trgs[ntrgs].v[2]
= vert_list[tri_table[cube_index][i+2]];
ntrgs++;
}
Основная часть
В обязательную часть задания входит реализация метода Wyvill или Lorensenдля нескольких динамических источников потенциала с расчетом нормалей. Обратите внимание, что это предполагает анимацию.
Дополнительная часть
1. Выбор размера сетки.
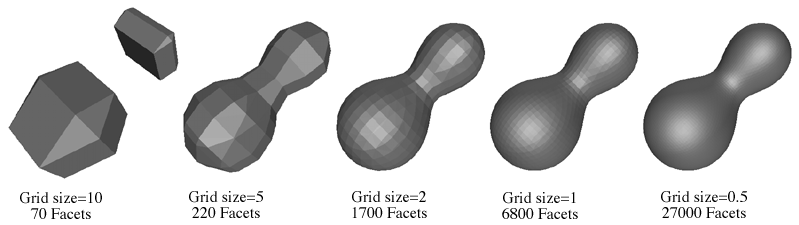
Размер сетки является первым
признаком улучшения качества и точности получаемой изоповерхности. Чем меньше
выбирается шаг сетки, тем больше получается вокселей, тем более гладкой и точной
получается результирующая изоперхность, но тем медленнее она будет
обрабатываться и рисоваться.
2. Вычисление нормалей.
Так как получаемая поверхность имеет довольно грубую треугольную
структуру, то, задавая нормаль только для треугольника (Flat
Normals) в целом мы получим резкий переход на границах треугольников.
Для этого используется метод Smooth Normals,
когда нормаль задается не для грани, а для вершины, и вычисляется в зависимости
от нормалей сходящихся в ней граней. На рисунке, расположенном ниже, показано
отличие этих двух методов.
(Flat
Normals).
(Smooth Normals)
 
3. Вопросы аппроксимации/интерполяции модели.
Если мы не хотим строить точную поверхность методом
Marching Cubes, а хотим получить лишь некое ее
приближение, при условии, что результирующая картинка будет гладкой,
можно воспользоваться следующим методом: методом Marching
Cubes на грубой сетке вычисляются контрольные точки, по которым затем
строится гладкая поверхность (например, с помощью
сплайнов). Ниже на рисунках показан результат применения данного подхода.
 
4. Структуры данных и управление потенциалами.
Естественно, что такие общие вопросы, как
раздельное хранение вершин и вокселей остаются в силе. В вокселе хранятся лишь
ссылки на вершины. Когда происходит движение потенциала, то происходит пересчет
значений потенциала только на вершинах и только в ограниченном объеме
пространства (ограничение по области действия потенциала). Для каждого
потенциала заранее просчитываются все возможные значения и в дальнейшем, при его
движение, происходит вычитание из старых точек и добавления потенциала к новым
точкам расположения потенциала. Конечно, потенциал можно аппроксимировать кубом
и использовать вычисления для всего куба (вычитание/добавление потенциала из
всех точек куба), но можно аппроксимировать шаром, используя быстрое
целочисленное (так у нас регулярная сетка) рисование сферы, которое основано на
целочисленным рисовании окружности и является всего-лишь его трехмерном аналогом
(два прохода вместо одного).
5. Визуализация нескольких изоповерхностей одновременно.
Под визуализацией нескольких полей одновременно подразумевается
одновременная визуализация полей для различных значений потенциала.
Соответственно, один поля будут находится внутри других, и увидеть их будет
возможно, только используя прозрачность. Но здесь сразу возникают проблемы.
Стандартные графические интерфейсы, такие как OpenGL
или DirectX реализуют прозрачность посредством
смешивания цветов, что в свою очередь требует отсортированность треугольников по
отношению расстояния к наблюдателя. Соответсвенно, для
корректной визуализации прозрачных скалярных полей необходимо доболнительно
реализовать сортировку получаемых треугольников, например, используя
BSP-tree (http://library.graphicon.ru/catalog/156)
6. Добавление отражений.
Значительно повышает качество картинки
добавление environment map текстуры на полученную
поверхность методом так называемого "хроматического" наложения текстуры
сферическим или линейным методом.

Литература.
1.
G. Wyvill, C. McPheeters, B. Wyvill "Data
structure for soft objects" Visual Computer (1986) 2: 227-234 (http://graphics.cs.msu.su/courses/cg_el01/wyvill.htm).
2.
W.E.
Lorensen and H.E. Cline,
"Marching
Cubes: A High.
Resolution 3D Surface Construction Algorithm",
Computer Graphics, vol. 21, no. 4, pp. 163-169, 1987.
3.
Эдвард Эйнджел "Интерактивная компьютерная графика. Вводный курс на базе
OpenGL,
2 изд.",
2001.
Требования к программе
Обязательное требование - выполнить обязательную часть задания.
Еще одно обязательное требование - разбираться в материале. В спорных
ситуациях оценка выставляется после личной беседы, выявляющей понимание принципа
действия основных алгоритмов.
К программе должны прилагаться все необходимые для ее запуска библиотеки.
(опускать можно только слишком большие библиотеки, если они явлются
стандартными). Отсутствие библиотек создает неудобства при проверке, однако не
фатально. У нас есть набор из наиболее часто недостающих библиотек для Borland
C++ Builder и MS Visual C++.
Примечание: glut32.dll в архив можно не включать.
Оценка
| Обязательная часть задания:
реализация метода Wyvill или Lorensen
(жесткий выбор точки) для нескольких динамических источников потенциала + расчет
нормалей. |
5 балла |
|
Интерполяционный выбор точки |
+1 балла |
| Плавный
расчет нормалей в вершинах. |
+2 балла |
| Аппроксимация
модели B-сплайном |
+3 балла |
| Наложение
"хроматической" текстуры |
+2 балла |
| Корректная
визуализация нескольких скалярных полей от каждого из источников посредством
прозрачности. |
+3 балла |
| Навигация |
+2 балла |
| Динамическое
изменение параметров источников полей, степени детализации и т.д. |
+2 балла |
Примечания:
- Указано максимальное количество баллов за каждую компоненту
- За каждый день опоздания снимается полбалла (округляется в большую сторону).
Работы с опозданием более чем на 12 дней не рассматриваются. Если у вас есть уважительная причина
опоздания, объясняйтесь с проверяющими лично.
Оформление работы
Оформление не отличается от обычного.
ZIP-архив с исходными текстами и исполняемыми файлами, названный по схеме
GZV_nnnnnnnn.zip (где G - последняя цифра номера группы, Z - номер задания, V -
номер версии задания, nnnnnnnn - номер студенческого билета) присылайте на
assign6@graphics.cs.msu.su
Например, студент 206 группы с номером студенческого билета 06529042, сдающий
обновленную (вторую) версию программы по второму заданию, должен прислать архив
с именем 622_06529042.zip.
Также смотрите здесь,
какие файлы
нам присылать и как их оформить Советуем очень внимательно прочитать весь
FAQ
Не забудьте положить в архив файл readme.txt. В файле описать интерфейс
программы (алгоритм работы с программой, пункты меню,
управляющие клавиши)
Результаты смотрите в интернете. Оценки появятся в течение двух недель после
срока сдачи задания.
Все вопросы присылать автору.
Примечания
- Задание выполняется строго индивидуально. За совместную работу или обмен
кусками кода ставится ноль баллов всем участникам, если факт командной
работы не был указан в readme.txt заданий.
- Не забывайте правильно оформлять исходный код ваших работ
ЧаВо по заданию
|
