Graphics & Media Lab. >> Курсы >> Курс Ю.М.Баяковского 1999

Illumination Models

local illumination 
defines single-light, single-surface interaction 
global illumination 
models interchange of lights between all surfaces 

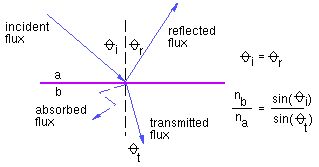
Local Illumination Models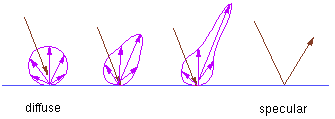 

Traditional graphics LIMs are: 

  • fast to compute 
  • heuristic and incomplete (non-physical) 
  • most interested in light in direction of viewpoint 
Most such adhoc illumination models have three components:  
 I = ambient + diffuse + specular
The ambient term allows for some global control of brightness in a scene. Typically,  
 I = Ia ka
where Ia is an ambient illumination constant defined once for the entire scene, and ka is an ambient reflection coefficient, usually restricted to lie in [0,1]. 

Diffuse Reflection 

  • Lambertian reflection 
  • apparent surface brightness independent of viewing angle 
  • distribution of scattered light is independent of direction of arriving light

 
 





Id = Ii k_diff cos(th), th in [-pi/2, pi/2]

    = Ii k_diff (N.L),   N.L  0 and assuming N and L are          normalized
Ii: intensity of light source i
k_diff: surface reflection coefficient
th: angle between N and L 

Phong Specular Reflection 

The last component of the commonly-used local illumination model is one that takes into account specular reflections. The following figure illustrates the situation:

The Phong illumination model is one often-used method of calculating the specular component:  

  Is = Ii k_spec cos^n(alpha)

     = Ii K_spec (R.V)^n
where k_spec is a specular reflection coefficient and alpha is the angle between the reflection and viewing vector. The surface parameter 'n' can be thought of as describing the surface roughness, where an ideal mirror would have n=¥ , and a rough surface might have n=1.

How can R be computed?  


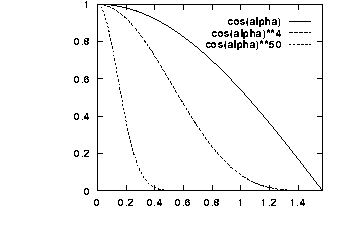
The function cos^n(alpha) looks as follows:







The Blinn Specular Model

Blinn reformulated the specular reflection model so that it agreed better
with experimental results. It makes use of a halfway vector, H, as follows:

Is = Ii k_spec cos^n(alpha)

     = Ii K_spec (N.H)^n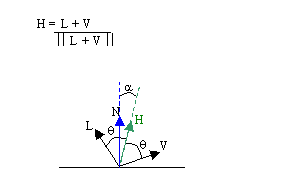

The advantages of
this model include:

    

  • 
theoretical basis
    • 


  • 
N.H cannot be negative if N.L>0 and N.V>0
    • 


  • 
for a directional light and an orthographic projection, H is constant
    • 





The Complete Model

Combining the various models and assuming the Phong illumination model
gives: 

I = Ia ka + Ii k_diff (N.L) + Ii k_spec (R.V)^n

where each of ka, k_diff, and k_spec are parameters which are associated
with specific surfaces and take on values between 0 and 1. To deal with
colour, three equations of the above form are typically used: 

I_r = Ia_r ka_r + Ii_r k_diff_r (N.L) + Ii_r k_spec_r (R.V)^n

I_g = Ia_g ka_g + Ii_g k_diff_g (N.L) + Ii_g k_spec_g (R.V)^n

I_b = Ia_b ka_b + Ii_b k_diff_b (N.L) + Ii_b k_spec_b (R.V)^n

Some other problems and their adhoc solutions: 




What should be done if I1? 




Clamp the value of I to one. 




What should be done if N.L < 0? 




Clamp the value of I to zero or flip the normal. 




How can we handle multiple light sources? 




Sum the intensity of the individual contributions. 











Shading Algorithms 






flat shading 




Invoke illumination model (IM) once for the polygon, use this as a colour
for the whole polygon 




Gouraud shading 




Compute IM at the vertices, interpolate these colours across the polygon




Phong shading 




Interpolate normals during scan conversion, apply IM at every pixel. (note:
renormalization problem) 






Problems with shading algorithms 



    

  • 
orientation dependence 
    • 


  • 
silhouettes 
    • 


  • 
perspective distortion 
    • 


  • 
T-vertices 
    • 


  • 
generation of vertex normals 
    • 





Lighting models in OpenGL 

The following are calls which set the parameters of a light: 

  glLightfv(GL_LIGHT0, GL_AMBIENT, amb_light_rgba );

  glLightfv(GL_LIGHT0, GL_DIFFUSE, dif_light_rgba );

  glLightfv(GL_LIGHT0, GL_SPECULAR, spec_light_rgba );

  glLightfv(GL_LIGHT0, GL_POSITION, position);

  glEnable(GL_LIGHT0);

The following calls define the surface properties to be used for all subsequently
drawn objects. 

  glMaterialfv( GL_FRONT, GL_AMBIENT, ambient_rgba );

  glMaterialfv( GL_FRONT, GL_DIFFUSE, diffuse_rgba );

  glMaterialfv( GL_FRONT, GL_SPECULAR, specular_rgba );

  glMaterialfv( GL_FRONT, GL_SHININESS, n );




Physics-based Illumination Models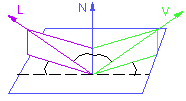 






    

  • 
BRDF: bidirectional reflectance distribution function
    • 











    

  • 
measuring BRDFs: gonioreflectometer 
    • 


  • 
analytical models 
    • 


  • 
statistical microfacet models 
    • 





Shadows 



    

  • 
projective rendering 
    • 


      

    • 
draw object a second time with additional shadow transformation 
      • 


    • 
darken existing image 
      • 


    • 
use stencil buffer to prevent `double shadows' 
      • 

    


  • 
raytracing 
    • 


      

    • 
part of method 
      • 


    • 
cast shadow ray 
      • 

    


  • 
area light sources 
    • 
















 





Graphics & Media Lab. >> Библиотека
 | Курсы | Графикон 












		Hosted by Graphics & Media Lab
	

	http://graphics.cs.msu.su
	
	

			

lab_logo




mailto:  Laboratory