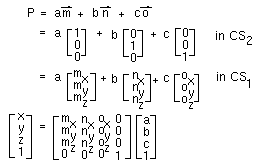| There is another way of looking at transformations which can let us
construct transformations between two coordinate systems directly, without
having to express the transformations in terms of one or more rotation
and translation operations.
Suppose we have two coordinate systems, CS 1 and CS 2, having coincident origins, but having different orientations:  The transformation between the two coordinate systems can be obtained
as follows.
The elements of the top-left 3x3 portion of any geometric transformation
are really the basis vectors of the local coordinate system expressed in
the coordinates of the new coordinate system.
|