Find the transformation that rotates by an angle theta about a point
P(x,y):
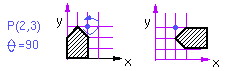 Let's choose to describe all transformations w.r.t. a fixed set of axes:
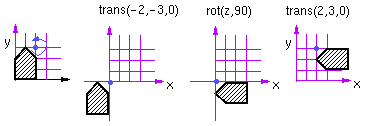 T = trans(2,3,0) rot(z,90) trans(-2,-3,0) Rotation about an arbitrary axis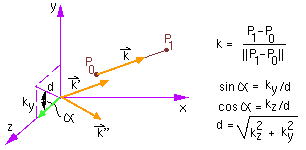
The amount of rotation is determined by looking at the projection on the yz plane. Alpha need not actually be calculated; it's sine and cosine can be evaluated directly. 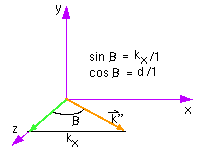 Overall Transformtrans(P0) rot(x,-alpha) rot(y,beta) rot(z,theta) rot(y,-beta) rot(x,alpha) trans(-P0) |