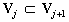 ,
,
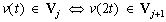 ,
,
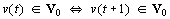 ,
,
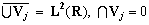 ,
,
- существует
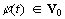 такая, что функции
такая, что функции 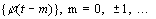 образуют ортонормированный базис пространства
образуют ортонормированный базис пространства 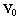 .
.
Введение в Вейвлет-Анализ
Лекция 2
Биортогональные вейвлеты, вейвлет-пакеты, сжатие изображений
Конструкция ортогональных вейвлетов
ОМА – это система подпространств ![]() ,
удовлетворяющая следующим условиям.
,
удовлетворяющая следующим условиям.
(2.1)
(2.2)
В качестве примера был приведен ОМА, порожденный функциями Хаара. Однако он имеет существенные недостатки. Дело в том, что, хотя скейлинг-функции и вейвлеты в явном виде не участвуют в алгоритмах разложения и восстановления, способность фильтров использовать имеющуюся в сигнале избыточность связана именно со свойствами этих функций – напомним, что они являются пределами при “бесконечной итерации” фильтров. Если сдвиги скейлинг-функции аппроксимируют гладкие функции лучше, чем негладкие, то гладкий сигнал будет лучше сжиматься – в векторе деталей будет много малых элементов. В изображениях, например, часто встречаются участки плавно меняющейся яркости. Функции Хаара не способны уловить такого рода избыточность.
Построение ОМА с гладкими базисными функциями сводится к построению
тригонометрических многочленов, удовлетворяющих (1.2’) и ряду дополнительных
ограничений (не любая пара QMF порождает ОМА). Найдя такой многочлен (т.е.
набор коэффициентов ![]() ),
можно вычислить скейлинг-функцию и вейвлет с любой точностью из (2.1) и
(2.2). Однако, как выяснилось, класс таких многочленов довольно узок, что
накладывает на свойства фильтров неудобные ограничения. В частности, они не
могут быть симметричными. Сейчас мы очень коротко наметим классический метод
построения таких фильтров, принадлежащий Ингрид Добеши (Ingrid Daubechies).
),
можно вычислить скейлинг-функцию и вейвлет с любой точностью из (2.1) и
(2.2). Однако, как выяснилось, класс таких многочленов довольно узок, что
накладывает на свойства фильтров неудобные ограничения. В частности, они не
могут быть симметричными. Сейчас мы очень коротко наметим классический метод
построения таких фильтров, принадлежащий Ингрид Добеши (Ingrid Daubechies).
Обозначим ![]() .
Должно выполняться условие:
.
Должно выполняться условие:
(2.3)
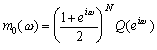 ,
, (2.4)
(2.5)
Требуется: а) найти многочлен ![]() ,
удовлетворяющий (2.5) и такой, что
,
удовлетворяющий (2.5) и такой, что ![]() при
при ![]() , и б)
извлечь из него квадратный корень в смысле (2.4). Ответ на а) предъявляется:
, и б)
извлечь из него квадратный корень в смысле (2.4). Ответ на а) предъявляется:
(2.6)
Показатель ![]() в (2.5) определяет степени полиномов, которые “убиваются” разложением по
построенному таким образом вейвлет-базису:
в (2.5) определяет степени полиномов, которые “убиваются” разложением по
построенному таким образом вейвлет-базису:
Эта величина называется количеством нулевых моментов (number of
vanishing moments). В классической конструкции Добеши длина фильтров ![]() ,
а количество нулевых моментов
,
а количество нулевых моментов ![]() .
На практике это означает, что фильтр
.
На практике это означает, что фильтр ![]() подавляет полиномиальную составляющую сигнала вида
подавляет полиномиальную составляющую сигнала вида ![]() ,
которая остается только в крупномасштабной версии. Например, для вейвлетов
Хаара
,
которая остается только в крупномасштабной версии. Например, для вейвлетов
Хаара ![]() , и
применение фильтра
, и
применение фильтра ![]() убивает постоянную составляющую сигнала.
убивает постоянную составляющую сигнала.