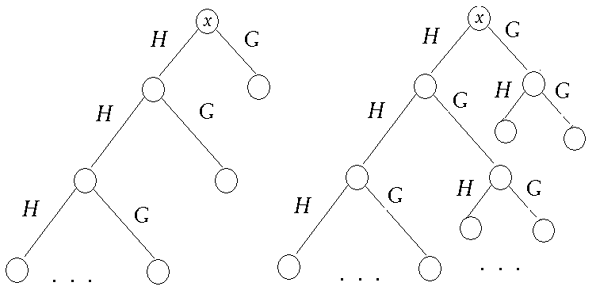
Похожую схему мы видели в самом начале первой лекции, когда говорили о квадратурных зеркальных фильтрах. Теперь ей можно дать истолкование на языке вейвлетов. Дерево на рис. 3 справа соответствует замене вейвлета  на два новых вейвлета:  и . Теперь разложение превращается в , где  и  порождены соответственно  и . Новые вейвлеты тоже локализованы в пространстве, но на вдвое более широком отрезке, чем исходный вейвлет, так как их локализация по частоте вдвое тоньше.

Можно нарисовать произвольное бинарное дерево разложения, и ему будет соответствовать набор подпространств с базисами, построенными по аналогичному рецепту. Функции, порождающие эти базисы, и называются вейвлет-пакетами (wavelet-packets). Ясно, что та же схема действует и в биортогональном случае.

На практике (при сжатии данных, например) мы имеем дело только с фильтрами. За счет выбора оптимального дерева для данного сигнала или класса сигналов иногда можно существенно (в несколько раз) повысить эффективность сжатия. Для выбора [квази]оптимального дерева разработан ряд методов. Все они основаны на введении некоторой функции (“энтропии”), позволяющей оценить “информативность” набора коэффициентов. Стратегия такова: сначала строится полное дерево разложения, затем снизу вверх анализируются пары узлов, имеющих общий корень. Если при переходе от корня к узлам энтропия не уменьшается, эта пара заменяется на корень. Упрощенный вариант – подобрать оптимальный уровень, т.е. высоту полного дерева, при которой энтропия минимальна.