Задание №1. Фрактальные изображения

Начало: 14 февраля 2002 года.
Конец: 27 февраля 2002 года (23:59)

Авторы задания:
Анастасия Куликова
Тимофей Уваров

Версия для печати здесь (zipped doc - 107кб)

Цель задания

Рассчитать (желательно с приемлемой скоростью) и отобразить фрактальное изображение.

Описание задания

Введение

Рассматривая некоторые последовательности комплексных чисел и выбирая закраску точки в зависмости от скорости сходимости последовательности, можно получить интересные изображения.

Обязательная часть

Здесь кратко рассмотрим наиболее простые методы генерации фракталов. Для выполнения задания достаточно реализовать какой-нибудь из них.

Построение множества Мандельброта

Рассмотрим последовательность комплексных чисел z_n и возьмем произвольное комлексное число c. теперь для каждого комлексного k рассмотрим последовательность вида z₀=k, z_n=z_n-1*z_n-1+c. Множество {k} таких, что данная последовательность стремится к нулю, называется множеством Жюлиа. Объединение всех связных множеств Жюлиа есть множество Мандельброта. Фракталы можно получить, строя множество Мандельброта и выбирая соответствующий способ раскраски. Подробнее об этом способе можно прочитать в описании задания за 2001 год. Вот один из примеров. Попробуйте сделать что-нибудь поинтереснее.

Также ищите дополнительные материалы в библиотеке курса. Описание множества Мандельброта приводится для полноты картины, но не является предметом этого задания.

Метод Ньютона

Другой пример. Он основан на решении уравнений методом Ньютона. Решение уравнения f(z) = 0 имеет вид z_k+1 = N(z_k), где N(z) = z - f(z)/f'(z). Рассмотрим уравнение pow (z, 3)-1 = 0. Вот как будет выглядеть построение фракталов, используя метод Ньютона для решения уравнения
maxIterations = 64;
count = 0;
z = current;//комплексные переменные
delta = z;
z1 = z;
while (count < maxIterations && abs(z) < 1e6
&& abs (delta) > 1e-6)
   {
   z = z - (z*z*z-1)/(3*z*z);
   delta = z1-z;
   z1 = z;
   }
SetColor (ColorPalette[count*256/maxIterations]); палитру можно сформировать по-разному, на данной картинке - градиентный переход цветов.

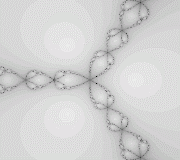
Рассмотрим этот метод более подробно. Возьмем рабочую область экрана S (равномерная двумерная сетка) как некоторую область G в комплексной плоскости (неравномерная двумерная сетка), то есть каждой точке (x,y) области S сопоставим точку (a,b) области G, так что a=L1(x) и b=L2(y), где L1 и L2 - линейные преобразования. Найдем корни уравнения (1) в области G, т.е. в каждой точке G (a0,b0) исследуем на сходимость итерационную последовательность {z_k} с начальным приближением z0=(a0,b0). Каждой точке (x0,y0) из S поставим в соответствие целое число C(x0,y0) из диапазона от 0 до 255 (или тройку чисел (r,g,b), где r,g и b - целые числа от 0 до 255), причем число C определяется в зависимости от того, сходится ли и как сходится итерационная последовательность {z_k} с начальным приближением z=(a,b), где a=L1(x0), b=L2(y0). Таким образом, получаем функцию от двух переменных C(x,y), которую можно рассмаривать как монохромное или цветное изображение или изображение в градациях серого. Различные варианты фракталов получаются варьированием параметра P1. Вот описание этого алгоритма на псевдокоде для всех точек рабочей области (x,y):  begin
     a=L1(x);
     b=L2(y);
     z0={a,b}; //z0-комплексное число
     z_prev=z0; //начальное приближение
     пока число итераций < MaxNumberOfIterations
         begin
         n=f(z_prev);
         d=f'(z_prev)+P1;
         z=z_prev-n/d;
         число итераций увеличить на 1;
     end
      if (|n|=0) SetPixel(x,y,0);
      else if (|n|=MaxPossibleValue) SetPixel(x,y,255)
      else // в зависимости от того, насколько далеко значение функции на элементе
      // последовательности от 0 после MaxNumberOfIterations итераций,
      // выбрать цвет в данной точке, например,
      SetPixel( x, y, |n|/MaxNumberOfIterations*255);
          // |n| - модуль комплексного числа, n=f(zk)
          // MaxPossibleValue - максимально возможное значение f(z) на итерационной
          // последовательности после MaxNumberOfIterations итераций
 end

Величины MaxNumberOfIterations и MaxPossibleValue выбитаются опытным путем. Например, можно взять MaxNumberOfIterations равным 100. Дополнительно прадлагается задать способ расцветки получившегося изображения. Алгоритм можно оптимизировать путем аппроксимации функций. Меняя параметры, можно получить различные интересные эффекты. Причем, если параметры отличаются незначительно, то картинки получающиеся при этих параметрах, тоже будут отличаться несильно. Таким образом можно получить плавные переходы между разными изображениями, сохранить их и создать видеопоследовательность.

Дополнительная часть

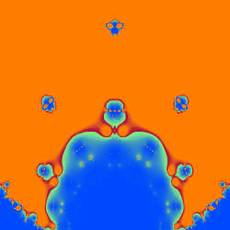
Более сложный пример задания последовательности комплексных чисел

Общая идея проста. Берется некая последовательность комлексных чисел z_n = F(z_n - 1), где F может быть суперпозицией различных функций. Рассматривается сходимость (расходимость) этой последовательности. Обычно достаточно рассмотреть около 30 итераций. Далее в зависимости от скорости сходимости выбирается цвет в точке. Рассмотрим пример с розой - расчет цвета в одной точке. Диапазон изменения комлексного числа current (1.41243196908302890000, 0.43820235769674321000) до (1.41299091299888270000, 0.43876197245340087000) Разность действительных частей соответствует ширине изображения, разность мнимых - высоте.
tolerance = 1e-6;
z = current;
zold = [0, 0];//комлексное число, Re(zold)=Im(zold)=0
xmax = xmin = xtot = 0;//вещественные числа
ymin = ymax = ytot = 0;
mmin = mmax = mtot = 0;
stop = 0;
//собственно вычисления
z += log (z);//комплексные функции
while (stop == 0 && count<30)//30 итераций достаточно
   {
  if (abs (Re(z)-Re(zold))<= tolerance
  && abs (Im(z)-Im(zold))<= tolerance)
  //критерий остановки
    stop = 1;
  else
    {
    sc = sec (z)*csc (z);//где sec(z)=1./cos(z), csc(z)=1./sin(z)
    f_z = log (sc);
    fp_z = 1/sc * (sc*tan(z)-sec(z)*pow(csc(z),2));
    zold = z;
    z = z - fp_z/f_z;//так определяется последовательность zn
    value = csc(z);
    //все что далее нужно для определения цвета
    x = Re (value);
    y = Im (value);
    m = abs(value);//модуль комл. числа - sqrt (x*x + y*y)
    xtot += x;
    ytot += y;
    mtot += m;
    xmin = min (xmin, x);
    xmax = max (xmax, x);
    ymin = min (ymin, y);
    ymax = max (ymax, y);
    mmin = min (mmin, m);
    mmax = max (mmax, m);
    count++;
  }
}
//теперь собственно определение цвета - немного изменив эту часть, получаем совсем др вид
r = g = b = 0;
if (count > 0)
  {
  r = ((xtot/count)-xmin)/(xmax-xmin);
  g = ((ytot/count)-ymin)/(ymax-ymin);
  b = ((mtot/count)-mmin)/(mmax-mmin);
  //параметры для расчета цвета, можно менять по-разному, но так
  // чтобы 0 < xStart < 255 и 0 < xStep < 2
  rStart = 255;
  gStart = 205;
  bStart = 255;
  rStep = 1.5;
  gStep = 1.5;
  bStep = 1.0;
  //собственно расчет цвета, здесь цвета как бы "идут по кругу"
  r = -cos (2*PI*r);
  g = -cos (2*PI*g);
  b = -cos (2*PI*b);
  r = r*127+127;
  g = g*127+127;
  b = b*127+127;
  r = r*rStep+rStart;
  g = g*gStep+gStart;
  b = b*bStep+bStart;
  r /= 360.0;
  g /= 360.0;
  b /= 360.0;
  r = sin (PI*r);
  g = sin (PI*g);
  b = sin (PI*b);
  r = r*128+127;
  g = g*128+127;
  b = b*128+127;
}
SetColor (b, g, r);

Метод Тейлора

Вот еще один достаточно простой метод. Рассмотрим разложение exp(z) в ряд Тейлора. Z - комлексное число. Фактически раскраска определяется тем, насколько быстро сумма многочленов, взятых с некоторым коэффициентом (в его выборе можно поэксперементировать), приближается к значению экспоненты. Вот пример, как это может выглядеть Расчет цвета в данной точке

maxIterations = 15;
tolerance = 1e-6;
z = exp (current);//current - точка на комлексной плоскости,
//соответствующая данной точке получаемого изображения
xmax = xdev = xavg = 0;
ymax = ydev = yavg = 0;
mmax = mdev = mavg = 0;
zSum = 0;
double denominator = 1;//вещественная переменная
point = exp (current);//это и будет весовой коэффициент
//совсем необязательно брать здесь экспоненту,
// выглядет это может и так point[5, 5]; point = sin (point)
// и т.д.
//цикл, не более maxIterations, пока zSum не подойдет "достаточно близко" к z
while (count < maxIterations && norm (zSum-z) > tolerance)
  {
  zSum += exp (point)*((current-point)^count)/denominator;
  if (count > 0)
    denominator *= (count+1);
   //теперь собственно определение цвета
   value = cot (zSum);
   x = abs (value^0.1);
   y = abs (value^0.2);
   m = abs (value^0.4);
   xavg = (x+xavg*count)/(count+1);
   yavg = (y+yavg*count)/(count+1);
   mavg = (m+mavg*count)/(count+1);
   xdev = sqrt ( (x-xavg)*(x-xavg) );
   ydev = sqrt ( (y-yavg)*(y-yavg) );
   mdev = sqrt ( (m-mavg)*(m-mavg) );
   xmax = max (x, xdev);
   ymax = max (y, ydev);
   mmax = max (m, mdev);
   xtot += xdev;
   ytot += ydev;
   mtot += mdev;
   }
r = g = b = 0;
if (count > 0)
   {
   r = (xtot/count)/ xmax;
   g = (ytot/count)/ ymax;
   b = (mtot/count)/ mmax;
   r = InterpolateColor (1, 255, r);
   g = InterpolateColor (1, 255, g);
   b = InterpolateColor (1, 255, b);
   }
SetColor (r, g, b);

Требования к программе

Обязательные требования

Дополнительные требования

Оценка

Оформление

Оформление не отличается от обычного.

ZIP-архив с исходными текстами и исполняемыми файлами, названный по схеме NMaaa_b.zip (где N-номер задания, M - номер группы, aaa - три первые латинские буквы фамилии, b - первая латинская буква имени) присылайте на assign1@graphics.cs.msu.su

Также смотрите здесь, какие файлы нам присылать и как их оформить Советуем очень внимательно прочитать весь FAQ

Не забудьте положить в архив файл readme.txt В файле указать следующие подзадания:

Метод построения: [указать метод(ы)]
Сохранение в файл: [+/-]
Масштабирование изображения: [+/-]
Анимация: [+/-]

Если вы реализовали какой-либо оригинальный метод, опишите его в комментариях.

!Внимание: обратите внимание на правильное именование и структуру архива с работой, а также на содержание файла readme.txt. Если ваша работа не будет соответствовать требованиям, баллы могут быть снижены.

Результаты работы

Результаты смотрите в интернете и/или на стенде около комнаты 703
Все вопросы присылать авторам и проверяющим .

Примечания

1. Задание выполняется строго индивидуально. За совместную работу или обмен кусками кода ставится ноль баллов всем участникам, если факт командной работы не был указан в readme.txt заданий.
2. Рекомендуется написание программы под семейство ОС Windows. Написание под другие операционные системы нежелательно и может вызвать задержки с проверкой таких работ.